Binding #2: The Michaelis-Menton Equation

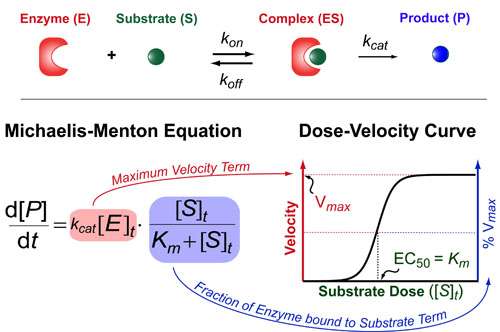
The Michaelis-Menton Equation has a very similar form to the Hill Equation but the key difference is that it deals with enzyme rates not ligand/receptor or drug/target interactions per se. Basically, it describes how fast an enzyme (E) makes its product (P) as a function of the total concentration of substrate ([S]_t). This rate of production formation (d[P]/dt) is proportional to the k_cat and the amount of complex ([ES]) which is exact what the Michaelis-Menton equation models. The Michaelis-constant (K_m = (k_off+k_cat) / k_on) describes how tightly the substrate binds the enzyme and the k_cat is a rate-constant that describes how quickly the enzyme can make the product. Here,brackets denote concentrations and a t subscript indicates “total concentrations.”

There are two parts to the Michaelis-Menton Equation. First, the maximum velocity term ([V]_max) which is equal to k_cat[E]_t. This term represents the maximum rate at which the enzyme can produce product (basically when the enzyme is saturated with substrate). Second, we have a fractional term which describes the shape of the dose-velocity curve in response to increasing concentrations of substrate. If you data is normalized to 100% then this fractional term is usually sufficient to describe your data.

On limitation of the Michaelis-Menton is that is only works when the receptor concentration is much lower than the Michaelis-constant (i.e. [R]_t << K_m). While this is often true experimentally (when very low concentrations of enzymes are ultilized), it is typically not true in vivo and a more general, quadratic-equation must be used as is described in a previous post: Understanding Ligand-Receptor Dose-Response Curves.

REFERENCES: 

1. Michaelis, V.; Menten, M. Die Kinetik der Invertinwirkung (The Kinetics of Invertase Action). Biochemische Zeitschrift 1913, 49, 33.
2. Johnson, K.; Goody, R. The Original Michaelis Constant: Translation of the 1913 Michaelis-Menten Paper. Biochemistry 2011, 50, 8265-8269.
3. Lineweaver, H.; Burke, D. The determination of enzyme dissociation constants. J. Am. Chem. Soc. 1934,56, 658-666.
4. Straus, O.H.; Goldstein, A.; Plachte, W. Zone Behavior of Enzymes. J. Gen. Physiol. 1943, 26, 559-585.
5. Cha, S. Kinetic Behavior at High Enzyme Concentrations. J. Biol. Chem. 1970, 245, 4814-4818.
6. Lauffenburger, D.A. Receptors: Models for Binding, Trafficking and Signalling, Oxford University Press 1993.
7. Segel, I.H. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems, Wiley-Interscience, 1993

This work by Eugene Douglass and Chad Miller is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.