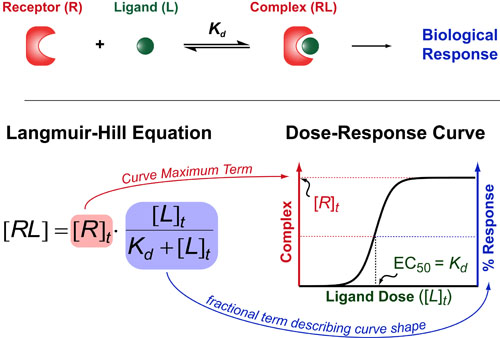
If you want to understand how drugs work/behave (or just how 2 molecules interact with each other) then you need to understand one of the oldest and most useful theories in biochemistry: the Hill Equation. The Hill Equation mathematically models how Ligands(L)/Drugs interaction with their Receptors(R)/targets and generally assumes that the amount of complex that forms (RL) is proportional to some biological response . Here the Kd represents the “dissociation constant” (which is a measure of the strength of the interaction between R and L) and brackets denote concentrations/dosages (with a t subscript indicating total concentrations).
The Langmuir-Hill Equation was co-discovered by the bio-chemisty Archibald Hill in 1910 and by the surface-chemist Irving Langmuir in 1916. Generally, this equation describes the shape of dose-response curves one obtains while titrating their drug or ligand of interest (bottom figure).
There are two parts to the Langmuir-Hill Equation. First, we have the total concentration of the receptor/target ([R]t). This term represents the maximum complex that can form and is generally proportional to the magnitude of the biological response you obtain (more complex = more downstream effect). Second, we have a fractional term which describes the shape of the dose-response curve in response to increasing concentrations of ligand/drug. If you data is normalized to 100% then this fractional term is usually sufficient to describe your data.
An interesting feature of this fractional term is that it defines the dose of ligand or drug which elicits a 50% maximal response or EC50 as being equal to the dissociation constant (Kd). This simple equation underlies all structure-based drug design approachs which endeavor to improve the clinical potency of a drug (EC50) by altering the chemistry so that it binding constant(Kd) improves.
On limitation of the Hill Equation is that is only works when the receptor concentration is much lower than the dissociation constant (i.e. [R]t << Kd). While this is true in most in vivo and cell-based experiments its sometimes breaks down in many biophysical experiment that require large amounts of protein. In these cases, a more general, quadratic-equation must be used in place of the Hill-Equation and is described in a previous post: Understanding Ligand-Receptor Dose-Response Curves.
REFERENCES:
- Hill, A.V. The possible effects of the aggregation of the molecules of haemoglobin on its dissociation curves. Proceedings of the Phsiological Society. 1910, 40, iv-vii.
- Langmuir, I. The Constituion and Fundamental Properties of Solids and Liquids. J. Am. Chem. Soc. 1916, 2221-2295.
- Lineweaver, H.; Burke, D. The determination of enzyme dissociation constants. J. Am. Chem. Soc. 1934,56, 658-666.
- Straus, O.H.; Goldstein, A.; Plachte, W. Zone Behavior of Enzymes. J. Gen. Physiol. 1943, 26, 559-585.
- Cha, S. Kinetic Behavior at High Enzyme Concentrations. J. Biol. Chem. 1970, 245, 4814-4818.
- Gesztelyi, R.; Zsuga, J.; Kemeny-Beke, A.; Varga, B.; Juhasz, B.; Tosaki, A. The Hill equation and the origin of quantitative pharmacology. Archive for History of Exact Sciences 2012, 66, 427-438.
- Goutelle, S.; Maurin, M.; Rougier, F.; Barbaut, X.; Bourguignon, L.; Ducher, M.; Maire, P. The Hill equation: a review of its capabilities in pharmacological modelling. Fund. Clin. Pharmacol. 2008, 22, 633-648.
- Lauffenburger, D.A. Receptors: Models for Binding, Trafficking and Signalling, Oxford University Press 1993.
- Segel, I.H. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems, Wiley-Interscience, 1993

This work by Eugene Douglass and Chad Miller is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.