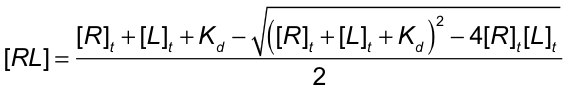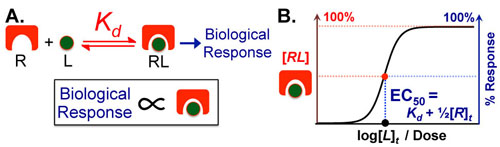
Figure 1 A.
Most Ligand (L)–Receptor (R) dose–response curves are characterized by formation of a complex followed by biological effect. The underlying assumption is that biological effect is proportional to the amount of complex that forms. B. Assuming the biological effect and amount of complex formed are proportional, dose–response curves can be envisioned on two equivalent axes: amount complex (in red) and percentage biological response (in blue). The key to intuitively understanding these curves is to understand the Effective Concentration 50% or EC50 which tells you the dose of ligand necessary to elicit a 50% response. The EC50 is also known as the ligand’s potency.
Biological phenomena are often caused by the binding of a ligand (L (e.g. drug, hormone, etc.)) to a target receptor (R), which induces a biological response (Figure 1A). Typically, the biological response is proportional to the amount of ligand-receptor complex (RL) that forms (Figure 1A); as a result, the dose–response curve can have two equivalent y-axes: amount of complex (in red) or biological response (in blue). These curves have a sigmoidal (S-like) shape, where low doses of ligand have no effect and high doses plateau at maximal (100%) complex formation/biological response (Figure 1B).
These curves can be mathematically defined by equations that can be useful for fitting or simulating the curves (as will be discussed in the next post). Unfortunately, these equations are relatively complex and so not very useful in intuiting how these curves behave. Instead, equations defining the half-maximun, or EC50 (Effective Concentration 50%), are significantly simpler and can capturing the position and shapes of these curves under different conditions. As defined in Figure 1B, the EC50 is equal to the sum of the dissociation constant (Kd) and one half the total concentration of target receptor (½[R]t) (Griffiths, J.R. Biochem. Soc. Trans. 1978, 6, 258).
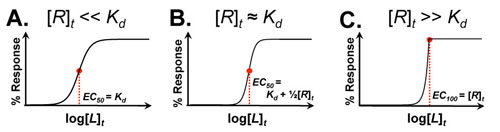
Figure 2. The Zone Behavior of Receptor–Ligand Dose–Response Curves. Zone A: The dissociation constant (Kd) dominates the curve’s behavior. Zone B: Both the dissociation constant (Kd) and the receptor concentration ([R]t) affect the curve’s behavior. Zone C: The receptor concentration ([R]t) dominates the curves behavior.
- ZONE A: Here, the dissociation constant alone defines the EC50 and you are in conditions or very low receptor concentration. In vivo drug targets, surface-based assays (e.g. ELISA, flow-cytommetry) as well as dilute enzymatic reactions very often fall under these conditions.
- ZONE B: Here, because the dissociation constant and receptor concentrations have similar values, the full equation for the EC50 must be used. Biophysical assays which require large amounts of protein/receptor such as Fluorescence Polarization or Isothermal Calorimetry often occur under these conditions. These curves are a bit steeper than those in Zone A.
- ZONE C: Here, the receptor concentration dominates the behavior of the curve and can be directly inspected at a saturated inflection point (or EC100). Very few systems occur under these conditions, as they require very large amounts of protein/receptor. Classically, such conditions have been used to determine stoichiometry.
When seeking to simulate or fit data obtained under conditions of Zone A, the Langmuir-Hill equation may be used. Unfortunately, this equations breaks down under the conditions of Zone B and C and a more complicated mathematical model must be used (Straus, O.H., et. al. J. Gen. Physiol 1943, 26, 559):
Later posts will describe (1) how to the use this complete equation in simulations and fitting, (2) how to intuitively understand competitive binding in terms of IC50s, and (3) the effect of spare receptors (where biological response is no longer directly proportional to complex formation) on sigmoidal dose response curves.
Receptor Ligand Curve Sheet PDF for mobile devices

This work by Eugene Douglass and Chad Miller is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.