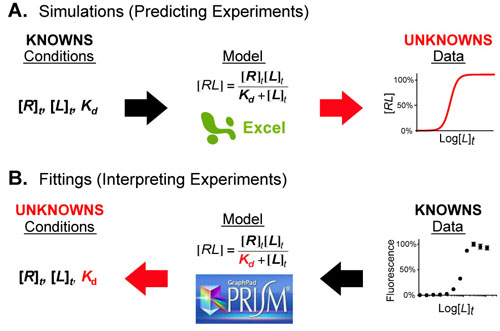
Figure 1. Mathematical models act as a bridge between the conditions of an experimental system and its behavior (the data). When a portion of either is unknown you can combine the knowns (black arrows) and calculate the unknowns (red arrows) using simple software packages such as Excel or Prism.
Mathematical models are equations (or systems of equations) that allow one the connect the conditions of a system/experiment with its predicted behavior/experimental data. Figure 1 shows an example of this where the Langmuir-Hill equation (in the center) connects the conditions (left) of a fluorescence binding assay with the dose-response curve (right) that results from conducting the experiment.
This “bridging” generally occurs in one of two directions:
- First, if complete information about your system is known (or can be estimated), it can be input into the equations of the mathematical model (using a software program such as Excel) in order to predict experimental results. This is known as a simulation
- Second, if some information about your experimental system is not known (such as the value of a dissociation constant, see above figure) you can calculate that unknown by combining your experimental data, the equation(s), and your known conditions using a program such as GraphPad Prism. This is known as curve fitting.
Mathematical Model Role PDF for mobile devices

This work by Eugene Douglass and Chad Miller is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
