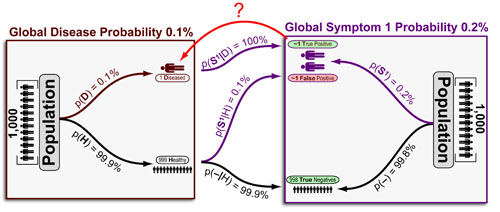
Baysian statistical inference is a very useful method to “back predict” the probability of a hypotheses from data frequency. In the example above, our “hypothesis” is “a disease“ and our “data” is the “an associated symptom.” Now, diseases are not measured directly, but rather, are diagnosed based on a combination of symptoms. Bayesian inference allows us to calculate the “Probability of Disease given Symptom 1 (p(D|S1)) with the following information:
- p(D) = 0.1%: frequency of the Disease
- p(S1) = 0.2%: frequency of the Symptom 1
- p(S1|D) = 100%: frequency of the Symptom 1 in the Diseased
as illustrated in the equations below:
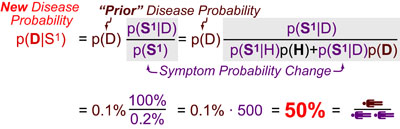
The key idea behind this equation is that the
- “change in disease probability given the symptoms” (p(D|S1)/p(D))
- “change in symptom probability given the disease” (p(S1|D)/p(S)1)
are equal. As a result, the above equation simply corrects the “Prior Disease Probability”(p(D)) using the “Symptom-Probability Change” (p(S1|D)/p(S)1). Interestingly, in the above example, even though the rate of symptoms in healthy individuals is very low (p(S1|H) = 0.1%) the fact that there are MANY more healthy individuals (p(H) = 99.9%) than diseased individuals (p(D) = 0.1%) exactly corrects for this enrichment which explains why only 50% of people with Symptom 1 have the Disease . Though idealized, this example demonstrates why a single symptom can rarely be used to conclusively demonstrate the presence of a disease.
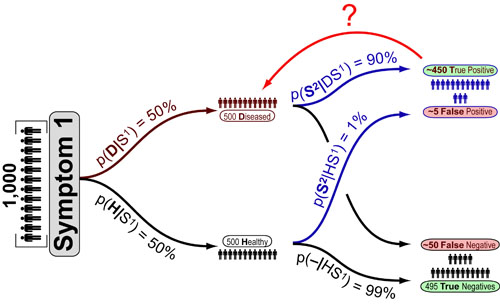
Along these lines, the true power of Bayesian analysis lies in its ability to “layer on” additional data without repeating preceding analysis. For example, based on the analysis above we know that out of the population with symptom 1, 50% have the disease(p(D|S1)) and 50% don’t(p(H|S1)). As can be seen in the diagram below, we can easily “layer on” frequency statistics associated with a second symptom (S2) to calculate the “Probability of Disease given Symptom 1 and Symptom 2 (p(D|S1S2)):

As you can see, the presence of a second symptom (even if only moderately enriched at 90%) dramatically increases the probability that the patient is suffering from a specific disease from 50% to 98.4% demonstrating the need for combinatorial disease-diagnoses in the clinic and combinatorial hypothesis-testing in the laboratory.
REFERENCES:
- Szallasi, Z.; Stelling J.; Periwal, V. System Modeling in Cellular Biology: From Concepts to Nuts and Bolts, 2006, The MIT Press

This work by Eugene Douglass and Chad Miller is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License