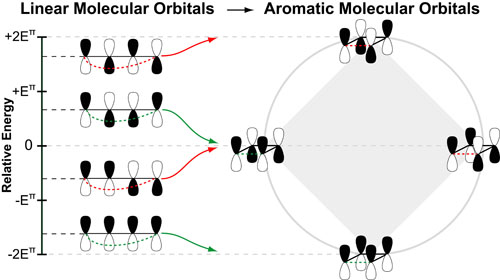
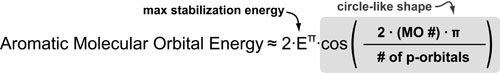Interestingly, once you understand the relative energies of linear pi-molecular orbitals the concept of “aromaticity” becomes alot simpler to understand. For example, cyclizing the frontier molecular orbitals (FMO) of butadiene gives you the anti-aromatic orbitals of cyclobutadiene. The “geometric arrangment” of these aromatic orbitals is a result of alternating stabilization (in green) or destabilization (in red) due to symmetry match or mismatch, respectively.1
This alternating stabilization/destablization is the source of Huckel’s rule where:
- AROMATIC SYSTEMS: the HOMO is stabilize in 4n+2 systems
- ANTI-AROMATIC SYSTEMS: the HOMO is destablized in 4n systems
In general, there is a maximum stabilization/destabilization energy associated with conjugated pi systems which is equal to 2 times the stabilization energy of a single pi-bond (2Eπ). This is the coefficient of the equation derived by Huckel below. In aromatic/cyclic systems, this maximum is reached by the lowest and highest energy frontier molecular orbitals.
The distribution of molecular orbitals between the minimum and maximum energies is defined by the cosine term in the equation below which gives this distribution a circular shape. A simple geometric trick to derive aromatic energies is to embed an equilateral shape with x sides (where x is the number of p-orbitals) into this circle with a vertex pointed down.
REFERENCES:
- McBride, J.M. Yale Chem 125: Freshman Organic Chemistry
- Huckel, E. Zeitschrift fur Physik, 1931, 70 204.
- Frost, A. A.; Musulin, B. Mnemonic device for molecular-orbital energies. J. Chem. Phys. 1953. 21, 572–573.
- Brown, A.D.; Brown, M. D. A geometric method for determining the Huckel molecular orbital energy levels of open chain, fully conjugated molecules. J. Chem. Educ. 1984, 61, 770.
- Fleming, I. Frontier Orbitals and Organic Chemical Reactions, Wiley-Interscience, 2004
- McQuarrie, D.A.; Simon, J.D. Physical Chemistry: A Molecular Approach. University Science Books, 1997