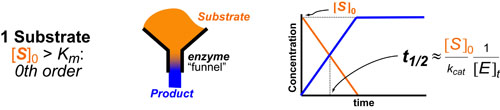
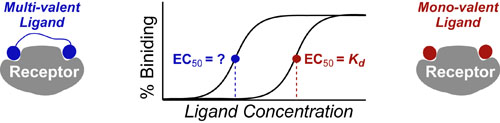
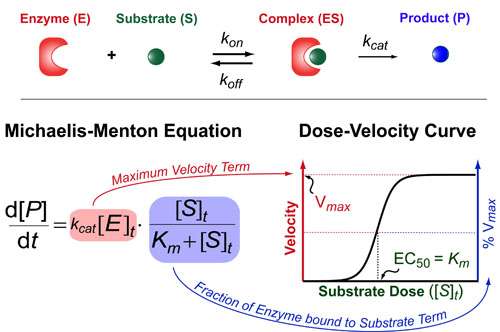
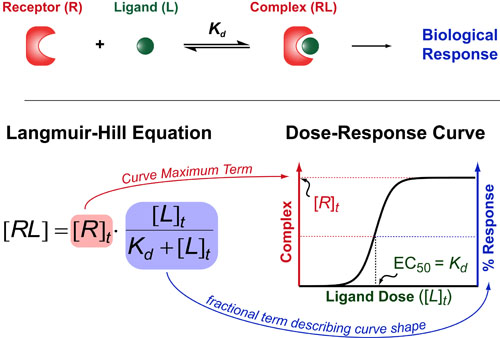
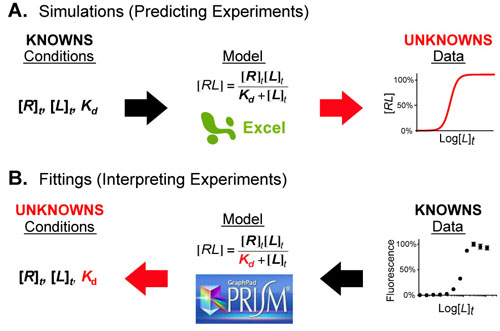
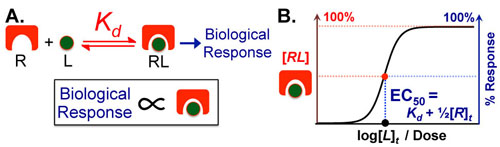
Most chemical and biochemical research concerns reaction that are catalyzed by either an enzyme or a chemical catalyst. Unfortunately, when we learn chemical kinetics, it is usually in the context of idealized: uncatalyzed 0th-order, 1st-order of 2nd-order chemical reactions. Luckily the intuition we learn from 0 and 1st order processes can be readily extended to catalyzed processes by invoking the pseuso-1st order approximation. Below we describe how to “think about” the most common enzymatic/catalytic kinetic curves you may encounter.
About Us
Practically Science was started by two Yale PhD students in 2012. Its goal is to make single-sheet summaries of common interdisciplinary methods, ideas, etc. Continue Reading →Please follow & like us :)
Blogroll
Site Map
-
Recent Posts