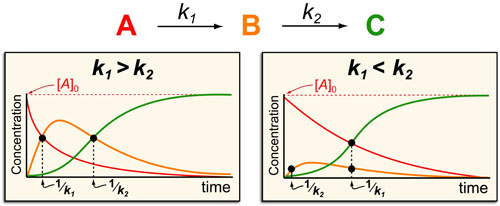
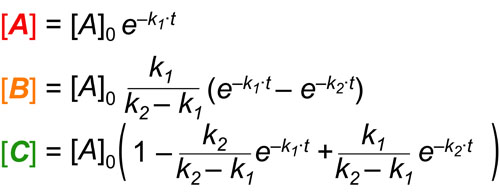In a follow up to our post our post on intuiting enzyme kinetics, we next wanted to consider the kinetic curves for sequential biochemical pathways. Luckily exact mathematical models exist for sequential first-order processes (see below) and we can use these to develop intuitive rules (figure above) if we consider these pathways to be approximately pseudo-first order (which is often true in the context of biosynthetic pathways).
In the scheme above, k1 and k2 represent the pseudo-first order rate constants for the conversions of A to B and B to C, respectively. In general, there are two possible scenarios when dealing with a sequential reaction that depend on if the first or second step is the fastest:
- k1 > k2 case: if the first step is faster than the second step then B forms with a timescale of 1/k1 and then decays as C forms with a time scale of 1/k2.
- k1 < k2 case: on the other hand, if the first step is slower than the second step then B barely forms at all and instead A decays and C forms with timescales of 1/k1.
Some general rules that fall out of this analysis are:
- The formation of products (such as C) occurs with a approximate timescale of 1/kRDS (where 1/kRDS is the rate constant for the slowest step in the upstream process)
- The decay of products (such as B or A) occurs with an approximate timescale of 1/kdecay (where 1/kdecay is the rate constant for the next step in the process (e.g. k1 for A and k2 for B))
REFERENCES:
- Segel, I.H. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems, Wiley-Interscience, 1993
- Banford, C.H.; Tipper, C.F.H. Comprehensive Chemical Kinetics. Elsevier, 1969
- McBane, G.C. Graduate Chemical Kinetics Lecture Notes. OSU875, http://faculty.gvsu.edu/mcbaneg/chem875.pdf
- Lauffenburger, D.A. Receptors: Models for Binding, Trafficking and Signalling, Oxford University Press 1993.

This work by Eugene Douglass and Chad Miller is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.