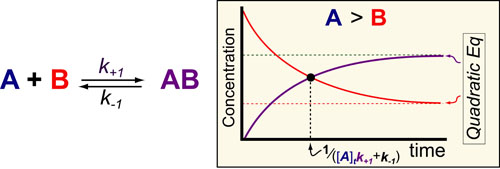
In our fifth post on Understanding Kinetics, we consider the speed at which molecular complexes form. This is the fundamental mechanism underlying drug action (i.e. drugs inhibition their targets) and cellular signalling (i.e. ligands activate their receptors) and is probably the most important “kinetic effect” to consider in experimental design. Here again we use previously derived mathematical models1 to define some simple rules for the timescales/half-lives and magnitude of these reactions (figure above).
In the scheme above, k+1 represents the second-order rate constant for A (drug) binding to B (target) and k-1 represent the first order rate constants for the dissociation of the complex AB and [A]t is equal to the total or initial concentration of A. The mathematical models are rather complex and described in detail in reference 1. However, if one assumes that the concentration of drug is greater than the concentration of target (see our post on the Hill Equation), several simple rules-of-thumb are obtainable.
- The timescale for formation of AB is approximately to 1 / ([A]tk+1 + k-1)
- The steady-state concentration of AB can be defined by the quadratic formula discussed in our post on Understanding Ligand-Receptor Dose-Response Curves
REFERENCES:
- Banford, C.H.; Tipper, C.F.H. Comprehensive Chemical Kinetics. Elsevier, 1969
- Segel, I.H. Enzyme Kinetics: Behavior and Analysis of Rapid Equilibrium and Steady-State Enzyme Systems, Wiley-Interscience, 1993
- Lauffenburger, D.A. Receptors: Models for Binding, Trafficking and Signalling, Oxford University Press 1993.

This work by Eugene Douglass and Chad Miller is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 3.0 Unported License.
